LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA NIESPODZIANKI DLA KLAS II GIMNAZJUM

Zadanie 2

Dane są okręgi zewnętrznie rozłączne. Wyznaczyć zbiór punktów takich, że dowolna prosta przechodząca przez taki punkt ma punkty wspólne z co najmniej jednym z tych okręgów.

Rozwiązanie

• Zobaczmy co będzie gdy punkt mogą leży na zewnątrz obu okręgów:

  

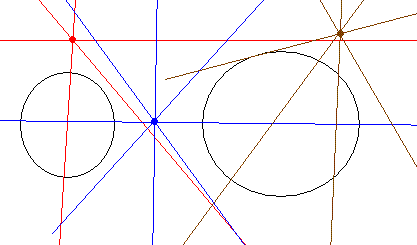
  Widzimy że zawsze można przez taki punkt poprowadzić prostą, która nie będzie się przecinać z żadnym z tych okręgów.

• Oczywiście punkty leżące na okręgu spełniają warunek zadania:

  

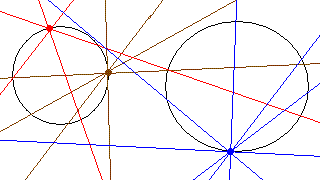
• Także punkty leżące wewnątrz któregoś z okręgów spełniają warunek zadania:

  

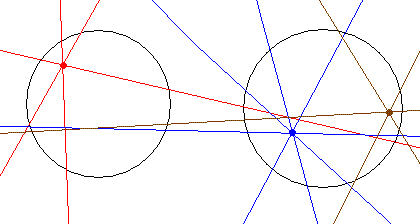
Odpowiedz: Zbiór punktów spełniających warunek zadania to dwa koła ograniczone danymi okręgami. obu okręgach.

Karol Romanowski