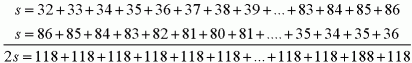
LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS I GIMNAZJUM

Zadanie 22

Czy można liczby naturalne od 32 do 86 włącznie wypisać w pewnej kolejności tak, by otrzymany zapis był zapisem liczby pierwszej?

Rozwiązanie

Dowiodę, że otrzymana liczba nigdy nie będzie liczbą pierwszą, ponieważ zawsze będzie się dzielić przez 11

Skorzystam w tym celu z cechy podzielności przez 11.
CECHA PODZIELNOŚCI PRZEZ 11: Dzielimy ciąg cyfr w zapisie dziesiętnym danej liczby na pakiety dwucyfrowe) na przykład pionowymi kreskami, w pakiecie lewej stronie może zostać 1 cyfra 2 cyfry) . Dodajemy otrzymane w ten sposób liczby i jeśli suma ta dzieli się przez 11 to dana liczba dzieli się przez 18.
Przykład:
1. Dana jest liczba 71973.
2. Dzielimy ja na " pakiety 2-cyfrowe 7|19|73.
3. Dodajemy: 73 + 19 + 7 = 99 dzieli się przez 11.
A więc liczba 71973 dzieli się przez 11.

Teraz widzimy, że w jakiejkolwiek kolejności nie wypisalibyśmy liczb od 32 do 86 to korzystając z powyższej cechy będziemy sprawdzali czy suma od 32 to 86 dzieli się przez 11.

Aby policzyć te sumę zastosuję magię w matematyce - dodamy w pierwszym rzędzie liczby od 32 do 86, a w drugim dodajemy liczby od 86 do 32. Co nam wychodzi zobaczcie sami:

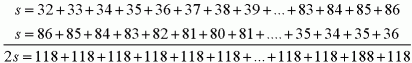
I pięknie nam wyszło suma górnej i dolnej liczby czyli s + s = 2s wynosi 118 razy ilość liczb od 32 do 86.
Co dalej?

Trzeba zobaczyć ile jest liczb od 32 do 86 włącznie. Wychodzi nam, że tych liczb jest 55, więc dwie sumy liczb od 32 do 86 dają tyle co 55 razy 118 czyli 6490. Zatem jedna taka suma równa jest 3245.

Teraz trzeba sprawdzić czy liczba 3245 dzieli się przez 11.

Tak jest, bo 3245 : 11 = 295 (bez reszty)

Paweł Sołtysiński