LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 22
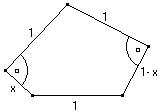
Oblicz pole wielokąta przedstawionego na rysunku wiedząc, że 0 < x < 1.
Rozwiązanie:
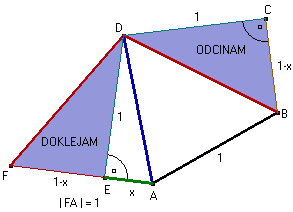
Przyjmując oznaczenia jak na rysunku mamy policzyć pole czworokąta ABCDE.
Jeśli jednak odetniemy od tego czworokąta trójkąt BCD i dokleimy go tak, że DC pokryje się z ED to trzymamy czworokąt FABD o tym, samym polu.
Czworokąt ten składa się z dwóch trójkątów ABD i FAD o bokach tej samej długości. Z cechy przystawania trójkątów (bok, bok, bok) wynika, że te trójkąty są więc przystające a co za tym idzie - mają to samo pole.
Pole trójkąta FAD jest równePFAD½×|FA|×|DE| = ½×1×1 = ½
Stąd:PABD = ½
Stąd:PFABD = PFAD + PABD = ½ + ½ = 1
Stąd:PABCDE = PFABD = 1
Odpowiedź:
Pole wielokąta wynosi 1 (w jednostkach kwadratowych).Paweł Sołtysiński