LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA NIESPODZIANKI DLA KLAS II GIMNAZJUM

Zadanie 5

Niech M będzie środkiem boku BC w trójkącie ABC, zaś N jest środkiem środkowej AM. Prosta CN przecina bok AB w punkcie K. Wyznaczyć .

Rozwiązanie

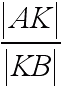Uwaga: Bedę kilka razy korzystał z twierdzenia o polach trójkątów (*). Twierdzenie to było przerabiane na kółku matenmatycznym.

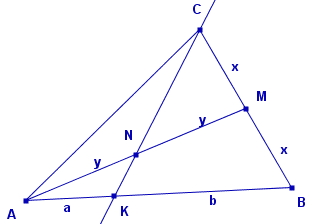
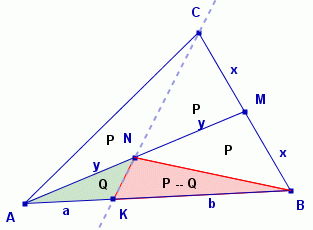
Sytuacja wygląda tak:

|AM|=|BM|=x,  |AN|=|NM|=y,    |AK|=a, |BK|=b

Trzeba policzyć a/b.

Narysujmy odcinek BN i niech P oznacza pole trójkąta BNM.

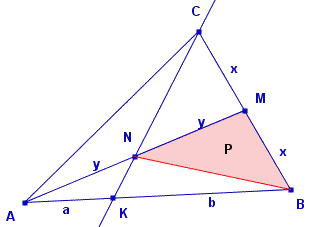P = PDBNP

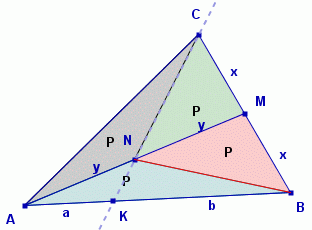(*) To samo pole P mają trójkąty zaznczone na rysunku:

P = PDBNM = PDCMN = PDCNA = PDANB

Niech Q oznacza pole trójkąta AKN. Wtedy pole trójkata BKN jest równe P - Q.

Wówczas:

(*)

oraz

(*)

Stąd

można teraz pooliczyć stosunek a do b:

Odpowiedź: .

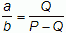
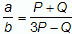
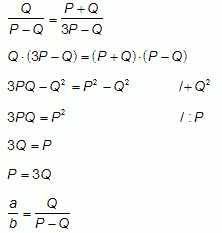
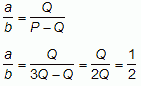
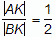Paweł Sołtyśiński