LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 23
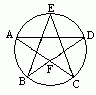
Na rysunku obok punkty A, B, C, D i E dzielą krąg na równe części. Oblicz miary kątów wpisanego CAD, kąta
CDE oraz kąta CFB.
Rozwiązanie
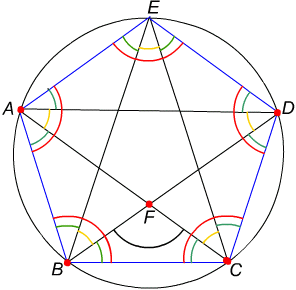 Dorysowane odcinki niebieskie ograniczają pięciokąt foremny ABCDE.
Dorysowane odcinki niebieskie ograniczają pięciokąt foremny ABCDE.
- Suma miar kątów w pięciokącie wynosi
(5-2) × 180° = 540°.
- Każdy kąt w pięciokącie foremnym ma
540° : 5 = 108°.
- W takim razie każdy kąt oznaczony na rysunku czerwonym łukiem ma 108°.
- Trójkąty CDE, DEA, EAB, ACB i BCD są równoramienne, więc katy przy jego podstawie mają po 36°
(bo 180° - 108° = 72° i 72° : 2 = 36°).
- Kąt CFB jest kątem wewnętrznym trójkąta BFC więc ponieważ dwa pozostałe katy w tym trójkącie mają po 36°, to sam kąt CFB ma miarę
180° - 108° = 72° i 72° : 2 = 36°.
Odpowiedź:
Kąt wpisany CDE ma 108°,
kąt CAD ma 36°,
kąt CFB ma 108°.
Joanna Suchecka


 Dorysowane odcinki niebieskie ograniczają pięciokąt foremny ABCDE.
Dorysowane odcinki niebieskie ograniczają pięciokąt foremny ABCDE.