LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA NIESPODZIANKI
DLA KLAS II GIMNAZJUM
Zadanie 7
Wiadomo, że w trapez można wpisać okrąg.
Na ramionach tego trapezu jako na średnicach konstruujemy okręgi.
Pokazać, że są one styczne zewnętrznie.
Rozwiązanie
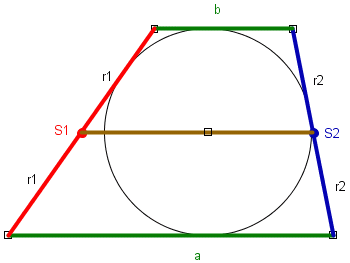
Niech S1, S2 będą środkami, a r1, r2 - promieniami okręgów skonstruowanych na ramionach trapezu jako na średnicach.
Wtedy S1, S2 są jednocześnie środkami ramion tego trapezu a 2r1, 2r2 są długościami jego ramion.
W czworokącie, w którym jest wpisane koło sumy przeciwległych boków muszą być równe, więc musi zachodzić równość:
2r1 + 2r2 = a + b
Stąd
r1 + r2 = ½ × (a + b)
Z drugiej strony długość odcinka łączącego środki ramion trapezu jest równa średniej arytmetycznej długości podstaw tego trapezu, a więc:
|S1S2| = ½ × (a + b)
Wynika stąd, że odległość między środkami okręgów jest równa sumie promieni tych okręgów.
|S1S2| = r1 + r2
| 
|
Oznacza to, że okręgi te są zewnętrznie styczne | 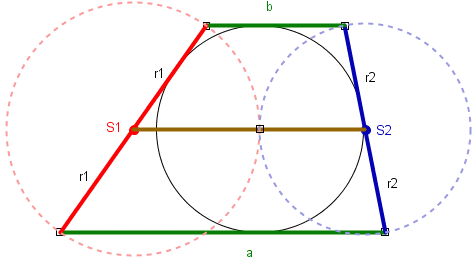
|
Marcin Swół

