Zadanie 8

Do dwóch okręgów przecinających się w punktach M i K prowadzimy wspólną styczną. Niech A i B będą punktami styczności tych okręgów i stycznej. Uzasadnić, że |ĐAMB| + |ĐAKB| = 180°.

Rozwiązanie:

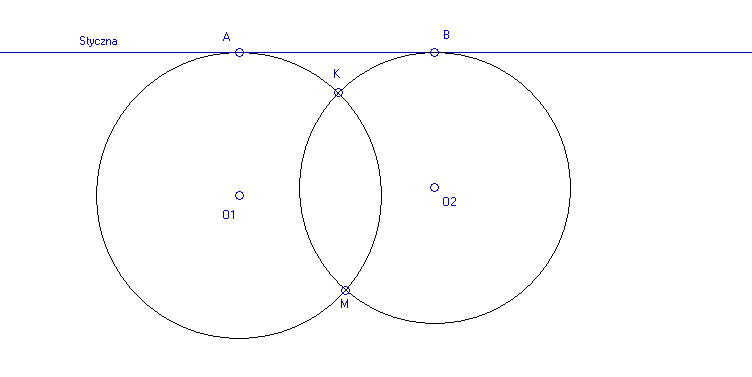
Rysunek:

Przyjmijmy oznaczenia jak na rysunku.

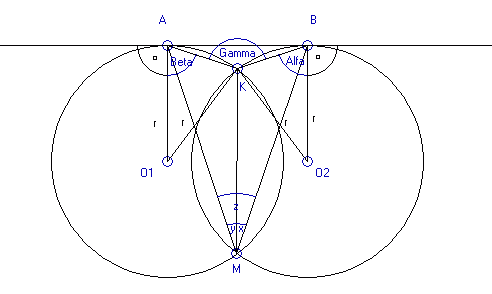
- Najpierw dorysowuję promienie okręgów poprowadzone do punktów styczności A i B. Czyli od pkt. O₁ do pkt. A oraz od pkt. O₂ do pkt. B. Tak więc można zaznaczyć kąty proste.

- Następnie znowu rysuję promienie okręgów, jednak tym razem od pkt. O₁ i O₂ do pkt. K.

- Łączę odcinkiem pkt. K i M oraz pkt. A i B z pkt.M i A i B z pkt. K.

- Kąty na tym rysunku oznaczam następująco: |AMK| = y, |KMB| = x, |AMB| = z, |KBO₂| = Alfa, |KAO₁| = Beta, |AKB| = Gamma.

Po wykonaniu tych czynności rysunek wygląda następująco:

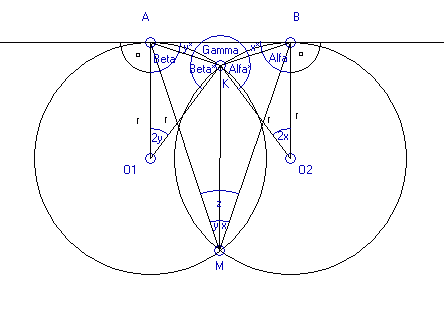
Kąt wpisany jest dwa razy mniejszy od kąta środkowego opartego na tym samym łuku, na tym rysunku mamy dwa kąty wpisane i środkowe. Pierwszy kąt wpisany to kąt |AMK| oparty na łuku AK i kąt środkowy również oparty na łuku AK to kąt |AO₁K|, natomiast drugi kąt wpisany to kąt |BMK| oparty na łuku KB oraz kąt środkowy to kąt |KO₂B| też oparty na łuku KB. Tak więc zaznaczamy odpowiednio kąty : 2y i 2x.

Kąt |O₁BA| również ma miarę Beta, ponieważ ramiona tego trójkąta są promieniami okręgu, więc są tej samej długości. Tak samo jest w przypadku kąta Alfa.

Teraz wiemy, że:

2Alfa + 2x = 180°

Alfa + x = 90°

Tak samo:

2Beta + 2y = 180°

Beta + y = 90°

Z czego wynika, że kąt |KAB| = y oraz, że kąt |KBA| = x.

Czyli z następującego równania wynika, że:

y + x + Gamma = 180°

(y + x) + Gamma = 180°

z + Gamma = 180°

Kąty |AMB| + |AKB| = 180°

Czego należało dowieść.

Całkowity rysunek wygląda następująco: