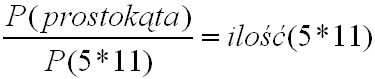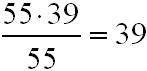LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA NIESPODZIANKI
DLA KLAS II GIMNAZJUM
Zadanie 3
Czy można prostokąt o wymiarach 55×39 pociąć na prostokąty o wymiarach 5×11?

1) Obliczamy pole dużego i małego prostokąta
Pole(prostokąta)= 55*39
Pole(małego prostokąta)= 5*11
2) Obliczamy ilość małych prostokątów które zmieszczą się w większym.
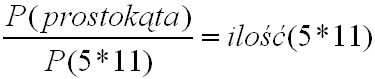
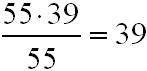
3) Niech
x- oznacza ilość ścian małego prostokąta o długości 5, odłożonych na boku o długości 39
y-oznacza ilość ścian małego prostokąta o długości 11, odłożonych na boku o długości 39
4) Wtedy x odcinków długości 5 oraz y odcinków długości 11 tworzą w sumie odcinek długości 39 więc musi być spełnione równanie:
x*5+y*11="39
dla y="1
5x+11*1="39
5x="28" - to równanie nie ma rozwiązania dla liczb naturalnych
dla y="2
5x+11*2="39
5x="17" - to równanie nie ma rozwiązania dla liczb naturalnych
dla y="3
5x+11*3="39
5x="6" - to równanie nie ma rozwiązania dla liczb naturalnych
Dalej nie trzeba sprawdzać, ponieważ x przyjeło by wartość ujemną, a skoro jest to długość odcinka jest to niemożliwe.
Odp.Nie da się tego zrobić
Tomasz Różyński IIa 2006/2007