LIGA ZADANIOWA UMK W TORUNIU 2005/2006
ZADANIA NIESPODZIANKI
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Zadanie 21
Treść zadania:
Pewna liczba dziewięciocyfrowa ma w zapisie
dziestiętnym wszystkie liczby oprócz zera. Po odpowiednim przestawieniu liczb
otrzymano liczbę 8 razy mniejszą. Wyznacz wszystkie liczby o powyższej własnośći.
Rozwiązanie:
Najmniejszą liczbąjaką można otrzymać z przestawienia cyfr od 1 do 9 jest 123456789.
Zauważmy, że 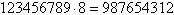
Każda inna permutacja cyfr od 1 do 9 da nam liczbę większą od 123456789, a więc
wynik mnożenia tej liczby przez 8 będzie większy od 987654312. Ale największa
liczba będąca permutacją cyfr o 1 do 9 to liczba 987654321, a ta nie
dzieli się przez 8*
Odpowiedź:
Jedyną liczbą, która ma wszystkie powyższe
własności jest liczba 987654312.
Michalina Rajczyk
*Zasada podzielności przez 8:
Liczba utworzona z trzech ostatnich
cyfr jest podzielna przez 8