LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie 21

 W czworokącie ABCD kąty wewnętrzne przy wierzchołkach B i D są proste oraz |AB| = |BC|. Wyznacz pole tego czworokąta przyjmując, że odległość wierzchołka B od prostej AD jest równa h.

Rozwiązanie:

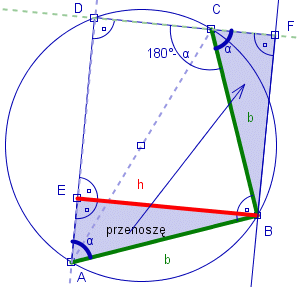
Rysunek 1
  1. Na czworokącie ABCD można opisać okrąg, bo kąty przy wierzchołkach B i D mają po 90°, czyli w sumie 180°.
  2. Rysuję prostą CD i prostopadle do nie prostą CF.
  3. Trójkąty AEB i CFB są przystające bo mają takie same kąty i taką samą przeciwprostokątną (gdyż |AB| = |BC|)
  4. Stąd |BF| = h i czworokąt ABCD ma to samo pole co kwadrat BFDE o boku h.
  5. Stąd czworokąt ABCD ma pole równe h2.

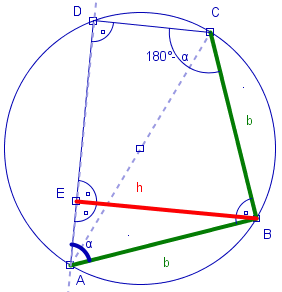
Rysunek 2

Odpowiedź:
Pole czworokąta ABCD wynosi h2 (jednostek pola).

Michalina Rajczyk