LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

Zadanie 1:

Średnicę okręgu AC podzielono na dwa odcinki AB i BC o długościach 12cm i 4cm. Na odcinkach tych zbudowano półkola jak na rysunku. Oblicz pole i obwód obszaru zakreskowanego (czarnego). Czy obwód tego obszaru jest większy o obwodu dużego okręgu?

Rozwiązanie:

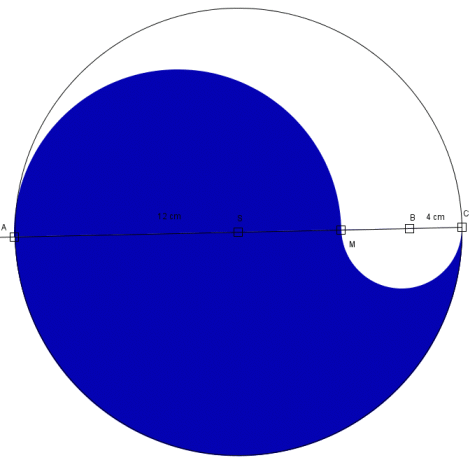
Pole wyznaczone przez kąt środkowy oparty na łuku AC nazwijmy a.

Pole wyznaczone przez kąt środkowy oparty na łuku AM nazwijmy b.

Pole wyznaczone przez kąt środkowy oparty na łuku MC nazwijmy c.

Możemy zauważyć, że pole zakreskowanej figury = a + b - c

P = a + b - c

gdzie...

a = ½×P×8²

b = ½×P×6²

c = ½×P×2²

a więc...

P = ½P8² + ½P6² - ½P2² = 48P

Długość łuku AC nazwijmy a'.

Długość łuku AC nazwijmy AM nazwijmy b'.

Długość łuku AC nazwijmy MC nazwijmy c'.

Możemy zauważyć, że obwód zakreskowanej figury = a' + b' + c'

Obw = a' + b' + c'

gdzie...

a' = ½×2P8

b = ½×2P6

c = ½×2P2

a więc...

Obw = ½×2P8 + ½×2P6 + ½×2P2 = 12P

Paweł Abramowicz