LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM
Zadanie 2
Ustaw w porządku rosnącym liczby: 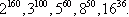
Rozwiązanie zadania:
1) Podstawy liczb podzielnych przez dwa można zapisać:
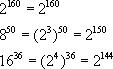
2) Powyższe liczby na osi liczbowej od liczby najmniejszej do największej wyglądają następująco:
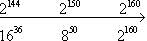
3) Teraz porównam liczby 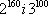 , aby dowiedzieć się, która z nich jest większa.
, aby dowiedzieć się, która z nich jest większa.
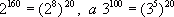
4) Teraz łatwo można obliczyć, która z liczb jest większa:
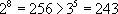
zatem
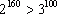
5) Przedstawiając na osi liczbowej liczbę 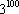 będzie się ona mieściła w przedziale:
będzie się ona mieściła w przedziale:
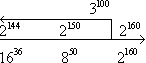
6) Teraz porównam liczby 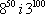 , aby dowiedzieć się, która z nich jest większa.
, aby dowiedzieć się, która z nich jest większa.
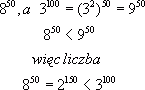
7) Tak więc liczba 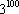 na osi liczbowej będzie wyglądała następująco:
na osi liczbowej będzie wyglądała następująco:
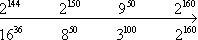
8) Pozostała nam tylko liczba 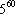 .
Najprościej by było ją porównać z liczbą
.
Najprościej by było ją porównać z liczbą 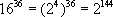 , bo wykładniki tych liczb mają wspólny dzielnik, mianowicie - 12.
, bo wykładniki tych liczb mają wspólny dzielnik, mianowicie - 12.
Można to zapisać tak:
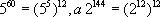
9) Teraz trzeba obliczyć:
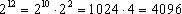
i
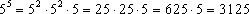
10) Stąd wiemy, że 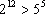 , więc liczba
, więc liczba 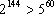 .
.
11) Tak więc liczba 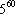 na osi liczbowej będzie wyglądała następująco:
na osi liczbowej będzie wyglądała następująco:
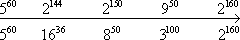
Odp.
Ustawienie liczb 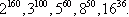 w porządku rosnącym wygląda następująco:
w porządku rosnącym wygląda następująco: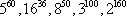
Stronę opracowała Katarzyna Błażejewska, uczennica klasy II "a"
Gimnazjum nr 11
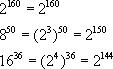
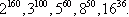
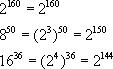
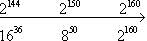
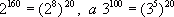
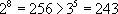
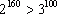
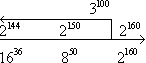
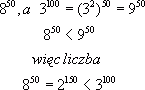
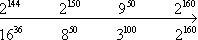
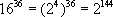 , bo wykładniki tych liczb mają wspólny dzielnik, mianowicie - 12.
, bo wykładniki tych liczb mają wspólny dzielnik, mianowicie - 12. 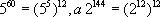
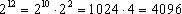
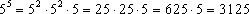
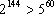 .
.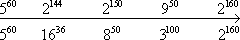
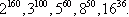 w porządku rosnącym wygląda następująco:
w porządku rosnącym wygląda następująco: