LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM

Zadanie 7a.

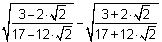
Oblicz: Root((3-2*Root(2))/(17-12*Root(2)))-Root((3+2*Root(2))/(17+12*Root(2)))

1. Na poczatku postanowiłem usunać niewymiernosć z mianownika (dla uproszczenia tymczasowo nie zamieszczałem tego w postaci pierwiastku):

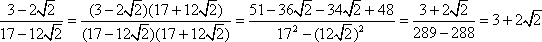
(3-2*Root(2))/(17-12*Root(2))=((3-2*Root(2))*(17+12*Root(2)))/((17-12*Root(2))*(17+2*Root(2)))=(51-36*Root(2)-34*Root(2)+48)/(17^2-(12*Root(2))^2)=(3+2*Root(2))/(289-288)=3+2*Root(2)

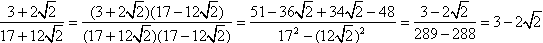
(3+2*Root(2))/(17+12*Root(2))=((3+2*Root(2))*(17-12*Root(2)))/((17+12*Root(2))*(17-2*Root(2)))=(51-36*Root(2)+34*Root(2)-48)/(17^2-(12*Root(2))^2)=(3-2*Root(2))/(289-288)=3-2*Root(2)

2. Następnie można zauważyć, że powyższe wyrażenia da się zamienić za pomoca wzorów skróconego mnożenia:

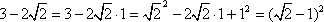
3-2*Root(2)=3-2*Root(2)*1=Root(2)^2-2*Root(2)*1+1^2=(Root(2)-1)^2

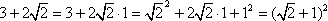
3+2*Root(2)=3+2*Root(2)*1=Root(2)^2+2*Root(2)*1+1^2=(Root(2)+1)^2

3. W punkcie 1. postanowiłem nie zamieszczać wyrażenia w pierwiastku, więc zrobię to tutaj, następnie podstawie zamiast niego wynik, który otrzymałem w 2. punkcie i uproszczę to wyrażenie:

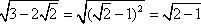
Root(3-2*Root(2))=Root((Root(2)-1)^2)=Root(2-1)

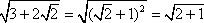
Root(3+2*Root(2))=Root((Root(2)+1)^2)=Root(2+1)

4. Pod koniec podstawiam w/w dane do działania:

Root((3-2*Root(2))/(17-12*Root(2)))-Root((3+2*Root(2))/(17+12*Root(2)))=(Root(2)+1)-(Root(2)-1)=Root(2)+1-Root(2)+1=2

Odp. Wynik to 2.

Opracował: Oskar Filipowicz