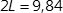
LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
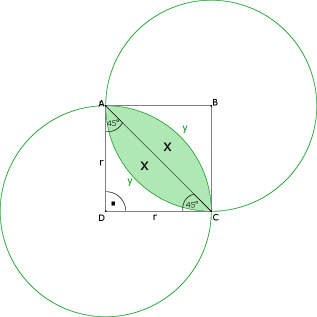
Rysunek pomocniczy:

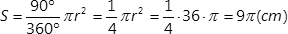
Wynik, który otrzymaliśmy jest to pole trójkąta ACD i x.
Aby otrzymać samo x musimy najpierw wyliczyć pole trójkąta i odjąć je od w/w wyniku.

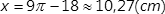
W ten sposób wiemy ile wynosi x, jednak pytanie było o całą część wspólną czyli 2x

2. Teraz odniesiemy się do 2. częci zadania czyli długości obwodu częci wspólnej. Skorzystam ze wzoru na długość łuku okręgu, na którym wspiera się kąt środkowy 
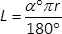
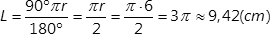
Otrzymaliśmy długość jednego łuku. Należy teraz pomnożyć to.