LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM

Zadanie 10

Uzasadnić, że 5ⁿ + 5ⁿ⁺¹ + 5ⁿ⁺² jest liczbą podzielną przez 155 dla każdej liczby całkowitej dodatniej n.

Rozwiązanie

Na początek chciałabym pokazać na przykładzie, że n nie może być liczbą całkowitą ujemną.

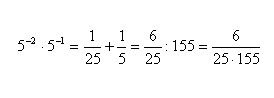
Następnie przekształcam podane w zadaniu wyrażenie.

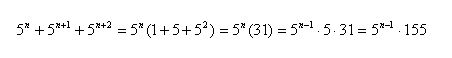
Ponieważ n jest naturalne i większe od zera, to n-1 jest większe lub równe 0. Zerowa potęga 5 jest jedynką, więc są spełnione warunki zadania. Dla każdej liczby n-1 większej od 0 otrzymana liczba jest iloczynem 131 i pewnejliczby naturalnej *w postaci potęgi liczby 5 o wykładniku 1, 2, 3 itd.)
To dowodzi podzielności przez 131.

Autorką tego rozwiązania jest Sandra Kisielewska.