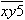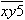LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS I GIMNAZJUM
Zadanie 12
Ile istnieje trzycyfrowych liczb przy zapisie których użyto tylko raz cyfry pięć?
Rozwiązanie zadania:
W każdej z tych trzy cyfrowy liczb piątka może występować:
- na początku (w miejscu setek)

- w środku (w miejscu dziesiątek)

- lub na końcu (w miejscu jedności)
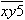
- Gdy cyfra 5 jest początku to za x można wstawić 9 cyfr i na każdą cyfrę x można wstawić 9 w miejsce y. (9 cyfr bo wszystkich cyfr jest 10 ale nie możemy ani za x ani za y wstawić cyfry 5).
Daje to 9×9 możliwości.
- Gdy cyfra 5 jest w środku to za x można wstawić 8 cyfr (bo x nie może być równe 0 i nie może być równe 5) i na każdą cyfrę x można wstawić 9 w miejsce y.
Daje to 8×9 możliwości.
- Gdy cyfra 5 jest w środku to za x można wstawić 8 cyfr (bo x nie może być równe 0 i nie może być równe 5) i na każdą cyfrę x można wstawić 9 w miejsce y.
Daje to 8×9 możliwości.
I wszystko to, do siebie dodać:
9×8 + 9×9 + 8×9 = 81 + 72 + 72 = 225
Odpowiedź: Istnieje 225 liczb trzycyfrowych przy zapisie których użyto tylko RAZ cyfry pięć.
Diana Kryczko