LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM
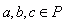
teraz przedstawmy za pomocą symboli jak będą wygladać i jakie warunki muszą spełniać nasze liczby i ich iloczyny:
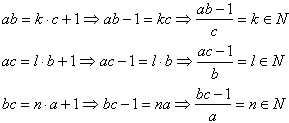
Iloczyn liczb naturalnych jest liczbą naturalną, więc: 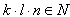
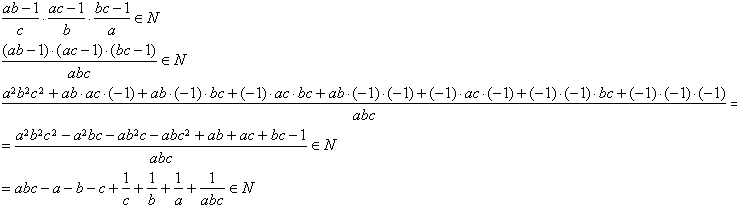
stąd 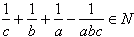
Możemy przyjąć, że: 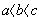 wtedy
wtedy 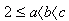
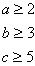 stąd
stąd 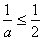
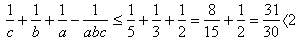
Wiedząc, że 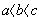 liczymy, że:
liczymy, że: 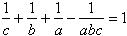 , ponieważ
, ponieważ 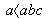 czyli
czyli 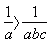
teraz musimy sprawdzić czy nasze założenia liczbowe będą się sprawdzać oraz w jakich kombinacjach. Zacznijmy od a:
a="2" 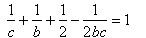
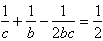
teraz dołóżmy do tego b="3"
a="2," b="3"
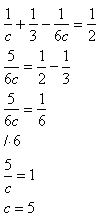
Zgadza się. Dla pewności wykonajmy sprawdzenie:
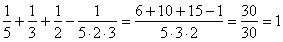
Spróbujmy utworzyć inną kombinację: a="2," b="5," a jeśli a="2" i b="5" to c>=7
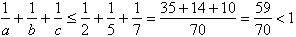 czyli nie zgadza się to z naszym wcześniejszym twierdzeniem.
czyli nie zgadza się to z naszym wcześniejszym twierdzeniem.
W takim wypadku spróbujmy zmienić liczbę a:
a="3," b>=5, c>=7 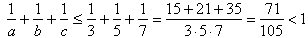
ta kombinacja również nie zgadza się z naszymi spostrzeżeniami, dlatego możemy wyciągnąć następujące wnioski:
Jeśli a>=3 to b>=5 i c>=7 to 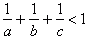 , więc niemożliwe jest, że
, więc niemożliwe jest, że 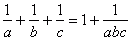
Zatem a musi równać się 2
jeśli a="2" i b>=5 to 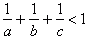
zatem a="2" i b="3" stąd c="5
Autor: Diana Kryczko