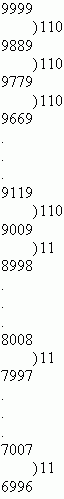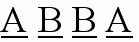LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS I GIMNAZJUM
Zadanie 13
2002 jest liczbą palindromiczną tzn. że czytana z lewej strony po prawej i odrwotnie z prawej do lewej jest tą samą liczbą. Poprzednią liczba palindromiczną jest liczba 1991. Jaka jest maksymalna odległość pomiedzy dwoma kolejnymi liczbami plalindromicznymi zawartymi wśród liczb od 1000 do 9999?
Rozwiązanie:
k = maksymalna odległość pomiędzy liczbami palindromicznymi wśród liczb od 1000 do 9999
ponieważ 9999 i 9889 są palindromiczne więc 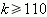 ,
,
co widać ponożej:
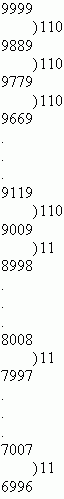
Liczba palindromiczna 4 cyfrowa jest postaci:
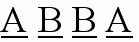
gdzie A Î {1, 2, 3, ..., 9} i B Î {0, 1, 2, 3, ..., 9}
- Jeśli B ą 9 to kolejna liczba palindowmiczna jest postaci:
A B+1 B+1 A
Po odjęciu liczby posatci A B B A otrzymamy 110:
A B+1 B+1 A
- A B B A
1 1 0
- Jeśli B = 9 to kolejna liczba palindromiczna jest postaci
A+1 0 0 A+1
Po odjęciu liczby posatci A 9 9 A otrzymamy 110:
A+1 0 0 A+1
- A 9 9 A
1 1
Teraz dokładnie widać, że największa różnica wynosi 110.
Jakub Kurowski
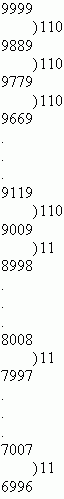
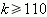 ,
,