LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA NIESPODZIANKI
DLA KLAS II GIMNAZJUM
Zadanie 14
W czworokącie ABCD, mamy . Przedłużenia boków BA i CD odpowiednio poza punkty A i D przecinają się w punkcie E, a przedłużenia boków AD i BC odpowiednio poza punkty D i C znadują się w punkcie F. Wiadomo, że |BE|=|BF| i Kąt DEF="25°." Znaleźć Kąt EFD.
Rozwiązanie:
- |BE|= |BF| więc trójkąt BEF jest równoramienny i stąd b = b'.
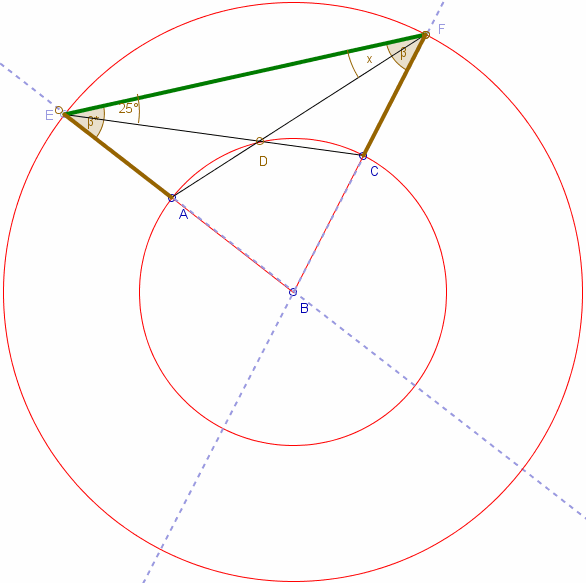
- |BE|= |BF| i |AB|=|BC| więc |AE|=|CF|.
Zatem z cechy bkb trójkąty AEF i CFE są przystajace i stąd x = 25°.
Odpowiedź: Miara kata EFD jest równa 25°.
Kusiński Łukasz

