Zadanie 20

LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

Zadanie 20

W trapezie dane są długości podstaw 10 cm i 30 cm oraz długości przekątnych: 24 cm i 32 cm. Oblicz pole tego trapezu jeżeli jego przekątne przecinają się pod kątem prostym.

Rozwiązanie

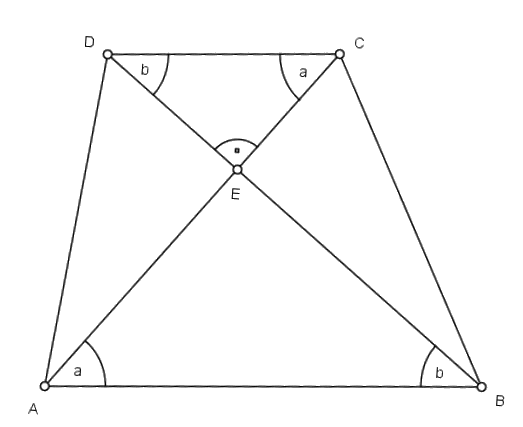
|AC|=24

|BD|=32

Oznaczamy kąty tej samej miary czyli a i b.

Z cechy KKK trójkąt ABE jest podobny do trójkąta ECD, więc:

|AB|:|BD|=|AE|:|EC|, dlatego 30:10=|AE|:|EC|

Z tego wynika, że:

30|EC|=10|AE| /:10

3|EC|=|AE|

|AE|+|EC|=4|EC|=24cm, dlatego:

|EC|=6cm i |AE|=18cm

Analogicznie |AD|=8cm i |EB|=24cm

P_ABCD=P_ABE+P_EBC+P_ECD+P_AED=

(18*24+6*24+6*8+8*18):2=216+72+24+72=384cm²

Odp: Pole tego trapezu wynosi 384cm²

Autor: Asia Pabich