LIGA ZADANIOWA UMK W TORUNIU 2006/2007
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS I GIMNAZJUM

Zadani 22

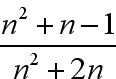Udowodnij, że jeśli n jest liczbą naturalną różną od 0, to ułamek: jest nieskracalny.

Rozwiązanie zadania:

Zakładając, że ten ułamek jest skracalny to licznik i mianownik mają wspólny dzielnik. Ich największy wspólny dzielnik oznaczę literą d. Czyli
  • Skoro n2 + n - 1 dzieli się przez d i n2 + 2n dzieli się przez d, to ich różnica także:

    n2 + 2n - (n2 + n - 1) = n2 + 2n - n2 - n + 1 = n + 1

    Więc n+1 dzieli się przez d.

  • Skoro n+1 dzieli się przez d to n(n+1) dzieli się przez d.

  • Skoro n(n+1) dzieli się przez d i n2 + n - 1 dzieli się przez d, to ich różnica też:

    n(n+1) - (n2 + n - 1) = n2 + n - n2 - n + 1 = 1

    Czyli d jest dzielnikiem liczby 1.

Jedynym dzielnikiem liczyby 1 jest liczba 1, więc d = 1.

Skoro d = 1, to znaczy że NWD(n2 + n - 1; n2 + 2n) = 1, to znaczy że ten ułamek można skrócić maksymalnie przez 1, to znaczy że jest to ułamek nieskracalny.

To już koniec, mam nadzieję że spodobało wam się moje rozwiązanie, życzę miłego rozwiązywania zadań!

Janusz Schmude kl.1a