ZADANIA KONKURSOWE Z ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 1
Oblicz pole i obwód zacieniowanych półksiężyców na rysunku obok wiedząc, że długość boku kwadratu wynosi 8 cm, zaś zewnętrzne łuki są półokręgami zbudowanymi na bokach kwadratu, a wewnętrzny łuk jest okręgiem opisanym na kwadracie.
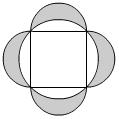
Rozwiązanie
a - długośc boku kwadratu, równa się 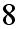
R - promień dużego koła, równa się połowie przekątnej kwadratu, tj. 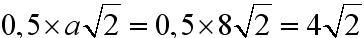
r - promień półkoła, jest połową boku kwadratu: 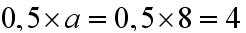
Obwód
Zauważmy, że obwód zacieniowanej figury to suma obwodów 4 półkoli i dużego koła. Wzór na obwód koła to 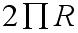 , a półkoła to
, a półkoła to 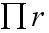 , więc:
, więc:
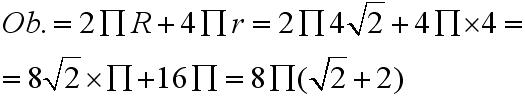
Pole
Zauważmy, że pole zacieniowanej figury to różnica sumy pola kwadratu z polem półkoli i pola koła. Wzór na pole koła to 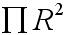 ,
półkoła to
,
półkoła to 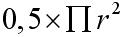 , a na pole kwadratu
, a na pole kwadratu 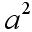 , więc:
, więc:
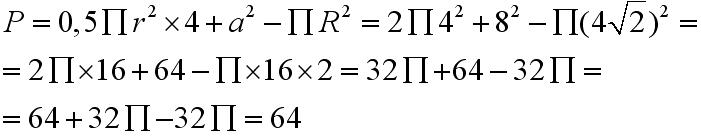
Odpowiedź:
Obwód półksiężyców wynosi 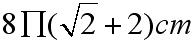 , a pole
, a pole
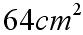 .
.
Opracował Filip Solarczyk
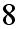

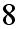
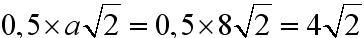
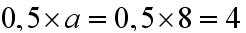
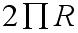 , a półkoła to
, a półkoła to 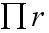 , więc:
, więc: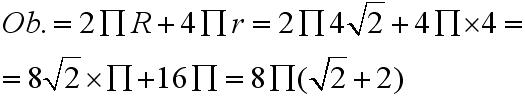
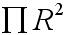 ,
półkoła to
,
półkoła to 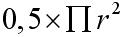 , a na pole kwadratu
, a na pole kwadratu 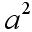 , więc:
, więc: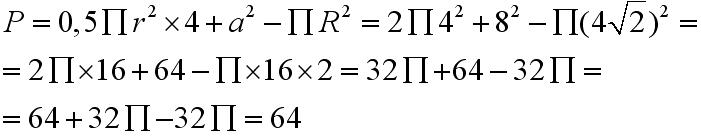
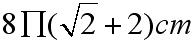 , a pole
, a pole
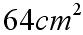 .
.