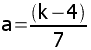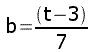LIGA ZADANIOWA UMK W TORUNIU 2007/2008
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS VI SZKOŁY PODSTAWOWEJ

Liczba k przy dzieleniu przez 7 daje resztę 3, więc

k = 7a + 4

gdzie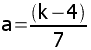

Liczba l przy dzieleniu przez 7 daje resztę 4, więc

t = 7b + 3

gdzie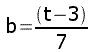

Jak się pewnie domyślamy liczby 7a i 7b są podzielne przez 7

Pomnóżmy obie liczby przez siebie.

k * t = (7a + 4)(7b + 3)
kt = 7a(7b + 3) + 4(7b + 3)
kt = 49ab + 21a + 28b + 12

Liczby 49ab, 21a, 28b są podzielne przez 7, toteż nie zostanie po nich reszta. Pozostaje nam tylko liczba 12. Nie może ona być resztą z dzielenia przez 7, więc trzeba odjąć od niej 7, które się podzieli.

12 - 7 = 5

Taka też będzie reszta.

ODPOWIEDŹ:  Iloczyn liczb K i T podzielony przez 7 da resztę 5.