ZADANIA KONKURSOWE Z ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie 5

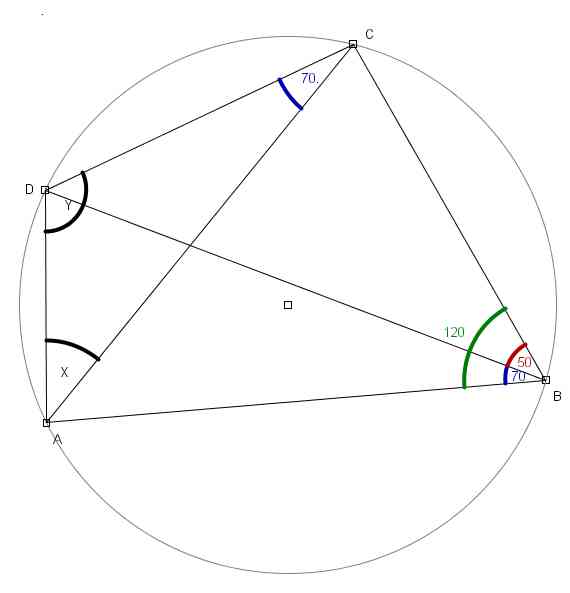
W czworokącie wypukłym ABCD dane są kąty: |ABC|=120°, |DBC|=50°, |ACD|=70°. Wyznacz kąty: |CAD|, |ADC|.

ROZWIAZANIE:

Od razu widzimy, że |ABD|=70°. Zatem |ABD| = |ACD|, więc okrąg opisany na trójkącie ACD będzie także zawierał punt B.

Stąd : |CAD|=|CBD|=X=50° bo katy CAD i CBD są oparte na tym samym łuku.

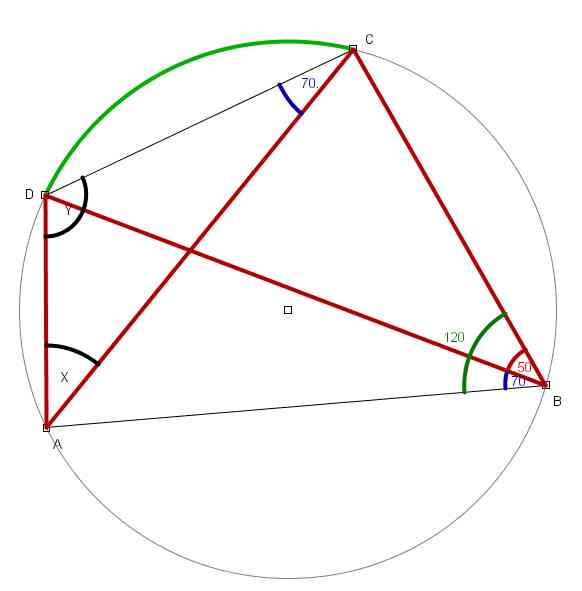
Wiedząc, że suma kątów w trójkoącie równa się 180° obliczamy kąt Y=|ADC|:

180°-|DAC|-|ACD|

180°-70°-50°=60°

Odp. Kąt |DAC| równa się 50°, a kąt |ADC| równa się 60°.

Maciej Urbański