LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 1
Oblicz pole i obwód zakreskowanych półksiężyców (patrz rysunek obok), gdzie długość boku kwadratu wynosi 8 cm, zaś zewnętrzne łuki są półokręgami zbudowanymi na bokach kwadratu, a wewnętrzny łuk jest okręgiem opisanym na kwadracie.
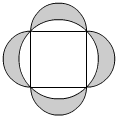
Rozwiązanie:
Obliczam pole kwadratu:
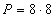
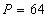
Następnie obliczam łączne pole czterech półokręgów o promieniu równym 4 cm:
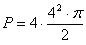
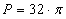
Obliczam długość przekątnej kwadratu:
Przękatna każdego kwadratu jest równa 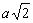 (przy czym a jest długością boku kwadratu):
(przy czym a jest długością boku kwadratu):
Długość przekątnej kwadratu = 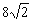 cm
cm
Obliczam długość promienia okręgu, który stanowi połowę przekątnej kwadratu na, którym jest opisany:
Długość promienia okręgu = 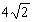 cm
cm
Obliczam pole okręgu:
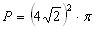
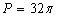
Od pola okręgu odejmuję pole wpisanego w niego kwadratu:
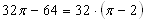
Otrzymane pole jest polem czterech niezacieniowanych półksiężyców.
Pole czterech zacieniowaych półksiężyców jest równe różnicy pól czterech półokręgów o promieniu równym 4 cm i pola czterech niezacieniowanych półksiężyców:
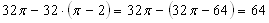
Pole jednego zacieniowanego półksiężyca jest równe:
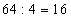
Pole zacieniowanego półksiężyca jest równe 16 cm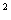 .
.
Obwód okręgu o promieniu 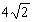 cm jest równy:
cm jest równy:
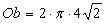
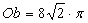
Obwód półokręgu o promieniu 4 cm jest równy:
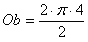
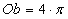
Obwód zakreskowanego półksiężyca jest równy sumie 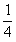 obwodu okręgu o promieniu
obwodu okręgu o promieniu 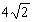 cm i obwodu półokręgu o promieniu równym 4 cm.
cm i obwodu półokręgu o promieniu równym 4 cm.
Więc obwód zacieniowanego księżyca jest równy:
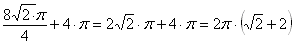
Odpowiedź:
Pole zacieniowanego jednego półksiężyca jest równe 16 cm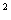 , a obwód jest równy
, a obwód jest równy 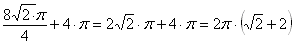 cm.
(Pole i obwód czterech zacieniowanych połksięzyców będą odpowiednio 4 razy wieksze. )
cm.
(Pole i obwód czterech zacieniowanych połksięzyców będą odpowiednio 4 razy wieksze. )
Tomek Bachanek

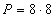
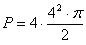
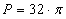
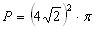
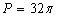
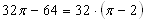
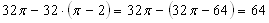
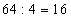
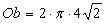
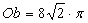
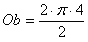
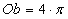
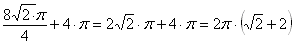
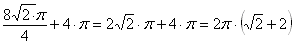 cm.
(Pole i obwód czterech zacieniowanych połksięzyców będą odpowiednio 4 razy wieksze. )
cm.
(Pole i obwód czterech zacieniowanych połksięzyców będą odpowiednio 4 razy wieksze. )