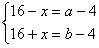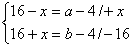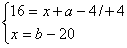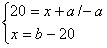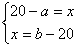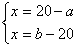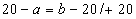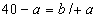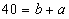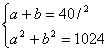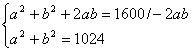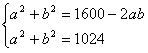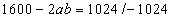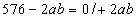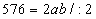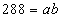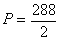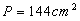LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 1:
Wyznacz pole i obwód trójkąta prostokątnego,w którym długość promienia okręgu wpisanego jest równa 4 cm i długość promienia okręgu opisanego jest równa 16 cm.
Rozwiązanie:
Najpierw wykonuję rysunek do zadania w którym środek okręgu o promieniu 16 cm nazywam "O", środek okręgu o promieniu 4 cm "P", a wierzchołki trójkąta prostokątnego "A", "B" i "C".
Zuważam, że przeciwprostokątna AC jest średnicą okręgu o środku "O". Długość przeciwprostoktnej AC jest równa dwóm promieniom okręgu o środku "O", więc:
|AC|=32 cm
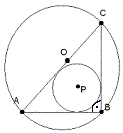
Następnie ze środka "P" prowadzę promienie do punktów styczności: "Q", "S", "T":
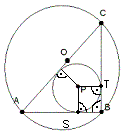
W ten sposób otrzymuję kwadrat o boku równym 4 cm.
Następnie łaczę prostą punkt "P" z puntkem "A" oraz punkt "P" z punktem "C".
W ten sposób otrzymuję 2 pary trójkątów przystających: trójkąt APQ i trójkąt QPS, trójkąt QPC i trójkąt PCT.
Z czego wynika, że |QA|=|SA|, |OC|=|CP|.
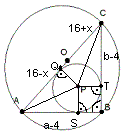
Wprowadzam długości odcinków: |QO|=x, |AQ|=16-x, |OC|=16+x, |AB|=a, |BC|=b, |AS|=a-4, |CT|=b-4.
Więc jeśli |QA|=|SA|, |OC|=|CP| to 16-x=a-4 i 16+x=b-4
Otrzymuję układ równań:
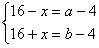
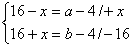
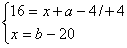
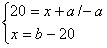
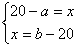
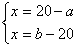
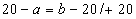
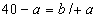
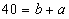
Obwód trójkąta ABC jest równy a+b+32 cm, więc:
Ob=40+32
Ob=72 cm
z Twierdzenia Pitagorasa:
|AB|2+|BC|2=|AC|2
a2+b2=322
a2+b2=1024
Otrzymuję kolejny układ równań:
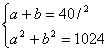
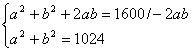
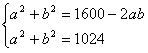
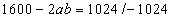
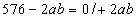
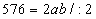
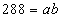
Pole trójkąta ABC jest równe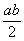 
, więc:
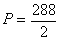
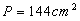
Odpowiedź:
Obwód trójkąta prostokątnego ABC jest równy 72 cm, a pole jest równe 144 cm2.
Tomek Bachanek