Zadania z ligi

LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie 3

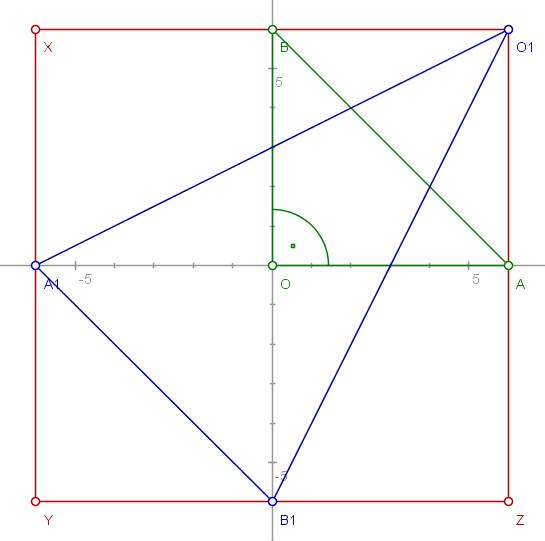
Dany jest trójkąt OAB, gdzie A="(6,0)," B="(0,6)" i O="(0,0)." Niech A1 będzie obrazem punktu A w symetrii osiowej względem prostej OB, B1 - obrazem punktu B w symetrii osiowej względem prostej OA i O1 - obrazem punktu O w symetrii osiowej względem prostej AB. Oblicz pole trójkąta A1B1O1.

Rozwiązanie:

Rysujemy kwadrat XYZO1.
Następnie obliczamy jego pole.
P_XYZO1=12*12="144[j2]
Kolejnym krokiem jest obliczenie pól trójkątów A1XO1, O1ZB1 i B1YA1.
P_A1XO1=1/2*12*6="36[j2]

P_O1ZB1=1/2*6*12="36[j2]

P_B1YA1=1/2*6*6="18[j2]
Na koniec od pola całego kwadratu odejmujemy pola trójkątów A1XO1, O1ZB1, B1YA1 i otrzymujemy pole trójkąta A1B1O1.

P_A1B1O1=144-36-36-18="54[j2]

Odpowiedz:

Pole trójkąta A1B1O1 wynosi 54[j²].

Ania Bekas 2a