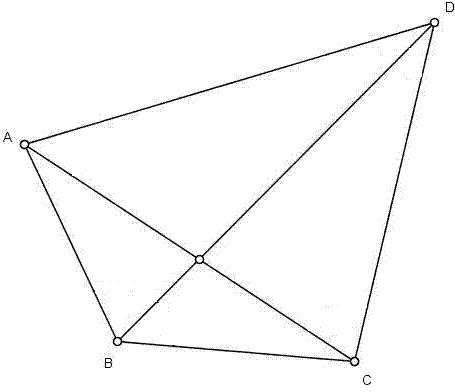
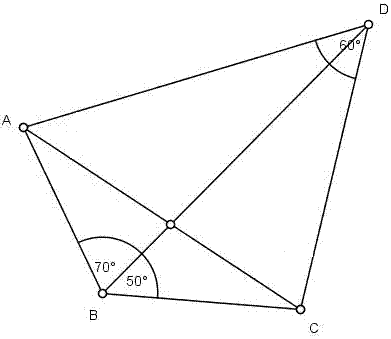
 Rysujemy czworokąt ABCD wraz z przekątnymi
Rysujemy czworokąt ABCD wraz z przekątnymi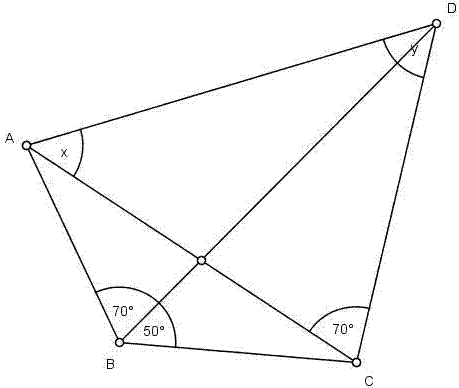 Zzaznaczamy kąty dane w zadaniu
Zzaznaczamy kąty dane w zadaniuLemat:
Jeśli kąty ACD i ABD są tej samej miary to punkty A, B, C, D leżą na jednym okręgu
Dowód
Niech K będzie okręgiem opisanym na trójkącie ADC.
| Gdyby punkt B leżał na zewnątrz koła to kąt ABD byłby mniejszy od kąta ACD | 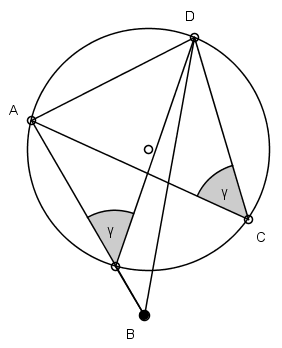 | a gdyby leżał wewnątrz koła to kąt ABD byłby większy od ACD. | 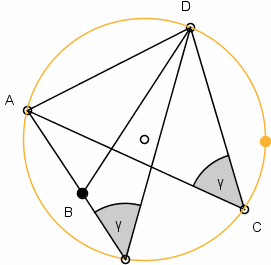 |
 Korzystając z lematu wiemy, że wierzchołki czworokąta leżą na jednym okręgu więc dwa naprzemianległe kąty czworokąta mają w sumie miarę 180°, więc kąt |ADC|=60°
Korzystając z lematu wiemy, że wierzchołki czworokąta leżą na jednym okręgu więc dwa naprzemianległe kąty czworokąta mają w sumie miarę 180°, więc kąt |ADC|=60°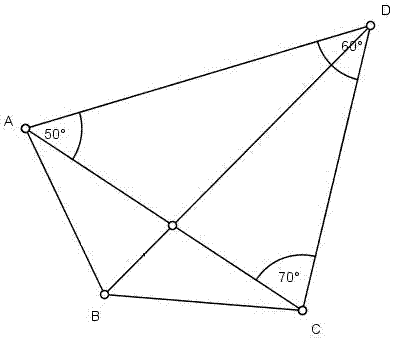 Wiemy, że wszystkie kąty w trójkącie dają 180° więc kąt |CAD|=50° stopni
Wiemy, że wszystkie kąty w trójkącie dają 180° więc kąt |CAD|=50° stopni
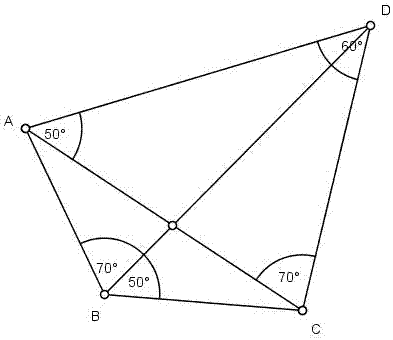 Oto efekt końcowy
Oto efekt końcowy