LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM
Zadanie 13
Uzasadnij, że liczba 5n+5n+1+5n+2jest liczbą podzielną przez 155 dla każdej liczby dodatniej n.
Rozwiązanie
5n+5n+1+5n+2=5n×(1+5+52)=5n×(1+5+25)=5n×(31)
155:31="5" czyli 31×5="155
n 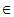 C+ (C + zbiór liczb całkowitych dodatnich) a więc n>0
C+ (C + zbiór liczb całkowitych dodatnich) a więc n>0
5 do jakiejś potęgi całkowitej dodatniej to wielokrotnośc piątki. Jeżeli z nawiasu wychodzi nam 31, a 31×5="155," to wielokrotnośc tego wyniku będzie podzielna przez 155.
Paulina Kużdowicz
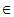 C+ (C + zbiór liczb całkowitych dodatnich) a więc n>0
C+ (C + zbiór liczb całkowitych dodatnich) a więc n>0