LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
ZADANIE 14
Uzasadnij, że w trójkącie prostokątnym suma długości przyprostokątnych jest równa sumie średnic okręgu wpisanego w ten trójkąt i okręgu opisanego na tym trójkącie.
ROZWIĄZANIE
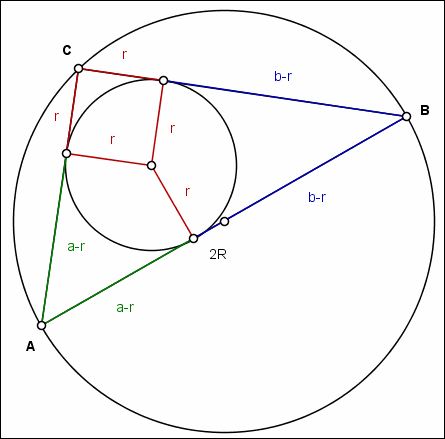
Oznaczenia na obrazku:
r - promień okręgu wpisanego w trójkąt
R - promień okręgu opisanego na trójkącie
a,b -długości przyprostokątnych
Twierdzenie:
Jeśli mamy dwie proste styczne do tego samego okręgu, przecinające się w punkcie P leżącym poza tym okręgiem, to odcinki od punktu P do punktów styczności są sobie równe.
Korzystając z powyższego twierdzenia można obliczyć:
(a-r)+(b-r)=2R
a+b-2r="2R" /+2r
a+b="2R+2r
Autor: Magdalena Kuźmicz 2a
