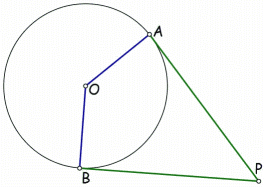
Wykorzystamy kilka razy twierdzenie (o odcinkach stycznych):Odcinki dwóch stycznych poprowadzonych do okręgu z danego punktu zewnętrznego P, wyznaczone przez ten punkt i odpowiednie punkty styczności A i B są równej długości
(patrz. rys. |PA|=|PB|)
LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Wykorzystamy kilka razy twierdzenie (o odcinkach stycznych):
Odcinki dwóch stycznych poprowadzonych do okręgu z danego punktu zewnętrznego P,
wyznaczone przez ten punkt i odpowiednie punkty styczności A i B są równej długości
(patrz. rys. |PA|=|PB|)
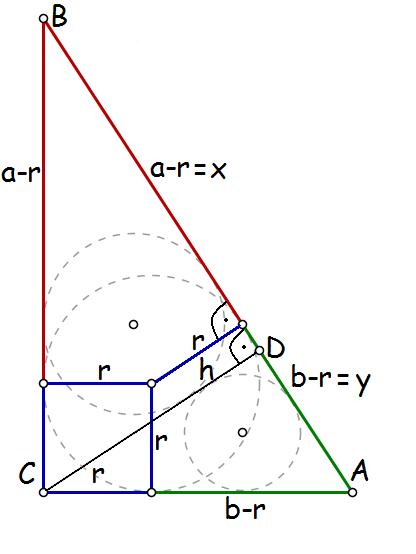
Onaczmy:
a =|BC|, b=|AC| - długości przyprostokątnych
r - promień okręgu wpisanego w trójkąt ABC
r 1 - promień okręgu wpisanego w trójkąt ADC
r 2 - promień okręgu wpisanego w trójkąt BCD
h - wysokość trójkąta czyli odcinek |CD|
x = a-r
y = b-r
Odcinki od wierzchołków to punktów styczności z okręgiem o promieniu r są równej długości i zaznaczone są tymi samymi kolorami
c = y + x
c = (b-r) + (a-r)
c = a + b - 2r
2r = a + b - c
Oznacza to, że:W trójkącie prostokątnym dwa promienie okręgu wpisanego równają się sumie przyprostokątneych minus przeciwprostokątna
Tę własność możemy zastosować nie tylko do trójkąta ABC ake także do trójkątów ADC i BCD,
czyli
2r = a + b - c
2r1 = h + |AD| - b
2r2 = h + |BD| - a
Stąd wynika, że:
2r + 2r 1 + 2r 2 = (a + b - c) + (h + |AD| - b) + (h + |BD| - a)Ale |AD| + |BD = c, więc
2r + 2r 1 + 2r 2 = 2h / :2Autor: Alicja Luboń 2a