LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM
Wyznaczyć liczby pierwsze p, dla których liczba 2p + 1 jest podzielna przez 9.
Zauważmy, że 2p przy dzieleniu przez 9 musi dawać resztę 8:
2p + 1 = 9n = 9n - 9 + 9 = 9(n - 1)+ 9
2p = 9(n - 1) + 8
Sprawdźmy, jaka będzie reszta dla dowolnych p: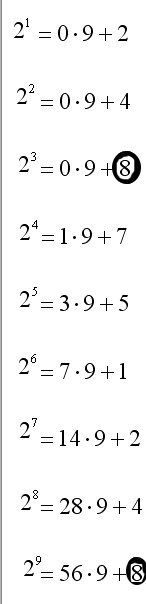
Dla dowolnego n wszystkie takie liczby dzielą się przez 3. a więc jedyną liczbą pierwszą wśród nich jest 3
Grzegorz Nehring