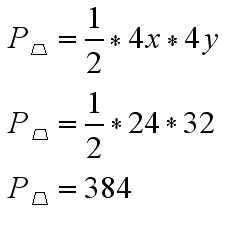LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
ZADANIE 17
W trapezie dane są długości podstaw 10 cm i 30 cm oraz długości przekątnych: 24 cm i 32 cm. Oblicz pole tego trapezu.
Rozwiązanie:
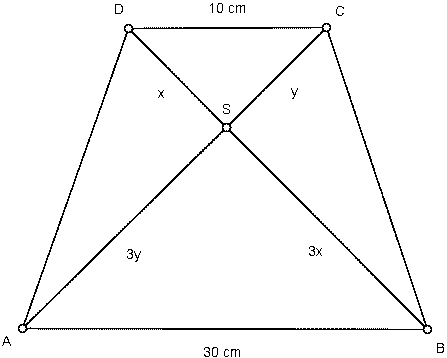 Trójkąty ABS i CDS są podobne w skali 3:1 ponieważ:
Trójkąty ABS i CDS są podobne w skali 3:1 ponieważ:
- miara kąta przy wierzchołku A = miara kąta przy wierzchołku D (kąty naprzemianległe)
- miara kąta przy wierzchołku B = miara kąta przy wierzchołku C (kąty naprzemianległe)
- skala = |AB|: |CD| = 30:10 = 3
Zatem jeśli w trójkącie CDS:
- przez x oznaczymy długość boku DS
- przez y oznaczymy długość boku CS
to:
- 3x jest długością boku BS
- 3y jest długością boku AS
Stąd długości przekąnych to:
- 4x - przekątna o długości 24 cm
- 4y - przekątna o długosci 32 cm
Stąd długości przekąnych to:
- 4x = 24 cm, stąd x = 6 cm
- 4y = 32 cm, stąd y = 6 cm
Z twierdzenia odwrotnego do twierdzenia Pitagorasa trójkąta CDS jest prostokątny gdyż
62 + 82 = 102
a to znaczy, że przekątne w tym czworokącie przecinaja się pod kątem prostym,
a w takich czworokątach pole jest równe połowie iloczynu przekątncych.
W takim razie pole trapezu ABCD możemy obliczyć w ten sposób:
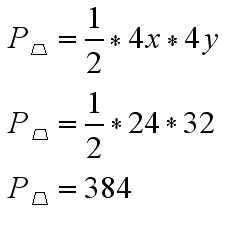
Odp. Pole trapezu ABCD wynosi 384 cm2.
Grzegorz Nehring
klasa 2a
Gimnazjum Nr 11
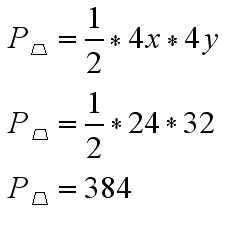
 Trójkąty ABS i CDS są podobne w skali 3:1 ponieważ:
Trójkąty ABS i CDS są podobne w skali 3:1 ponieważ: