LIGA ZADANIOWA UMK W TORUNIU 2008/2009
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 18a
Brzeg trójkąta równobocznego boku długości 10 cm "otoczono" zbiorem punktów, z których każdy jest odległy od jednego z boków nie więcej niż 1 cm. Oblicz długość brzegu tego zbioru i pole tego zbioru.
Rozwiązanie:
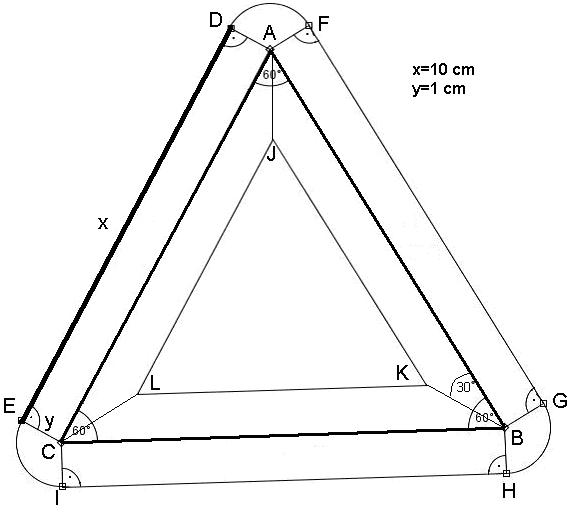
I. POLE
Widzimy, że pole zbioru od zewnętrznej strony trójkąta ABC składa się z 6 części: 3 prostokątów o wymiarach x="10" cm i y="1" cm,
oraz z trzech równych sobie wycinków koła, które tworzą jedno koło.
Więc pole zbioru od zewnętrznej strony trójkąta równa się:
PZew= 3*Pprostokąta + Pkoła
czyli:
PZew= 3*(1cm* 10cm) + 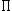 *1cm2=
*1cm2=
PZew= (30 +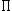 ) cm2
) cm2
Z kolei zbiór od wewnętrznej strony trójkąta ABC można podzielić na 3 trapezy:
trapez AJKB , trapez CLKB i na trapez CLJA.
Każdy z tych trapezów możemy podzielić na prostokąt i 2 równe sobie trójkąty prostokątne.
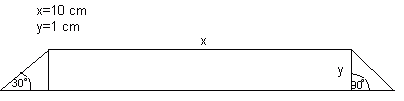
Wiadomo, że jeśli w trójkącie prostokątnym miary pozostałych 2 trójkątów są równe 30 i 60 stopni,
to długości boków wynoszą :
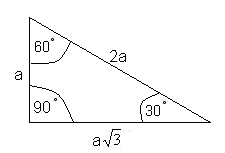
A skoro a="1" cm, to :
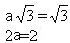
Więc wygląda to tak:

Pole tego trapezu równa się suma podstaw razy wysokość podzielić na dwa:
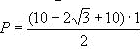
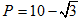
Więc pole zbioru od wewnętrznej strony trójkąta ABC równa się:
PWew= 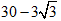
Więc pole całego zbioru(zewnętrznego i wewnętrznego) wynosi:
PCałość= 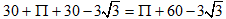
II. OBWÓD
Długość linii brzegowej od zewnętrznej strony trójkąta ABC równa się:
ObZew= 3*10 + 2* 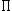 *1 = 30 + 2
*1 = 30 + 2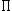
Teraz obliczymy długosć linii brzegowej od wewnętrznej strony trójkąta ABC:
ObWew= 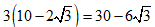
Więc łączna długość linii brzegowej wynosi:
ObCałość= ObZew + ObWew
ObCałość= 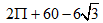
Odpowiedź:
Pole tego zbioru wynosi 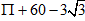 cm2,
cm2,
a długość linii brzegowej wynosi 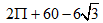 cm.
cm.
Mateusz Pacholski, klasa 2a gimnazjum^^
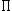 *1cm2=
*1cm2=
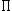 *1cm2=
*1cm2=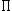 ) cm2
) cm2

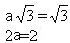

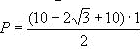
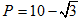
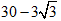
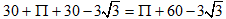
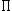 *1 = 30 + 2
*1 = 30 + 2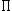
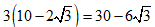
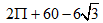
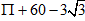 cm2,
cm2, 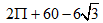 cm.
cm.