LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA WAKACYJNE
DLA UCZNIÓW GIMNAZJUM

Zadanie 20

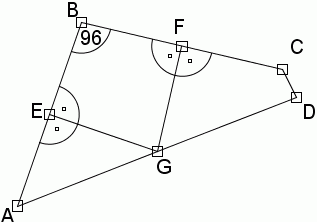
W czworokącie ABCD punkty E,F i G są odpowiednio środkami boków AB,BC i AD.

Rozwiązanie

1.Skonstujmy czworokąt, który będzie spełniał wszystkie warunki:

2.Musimy wyznaczyć kąt ACD:

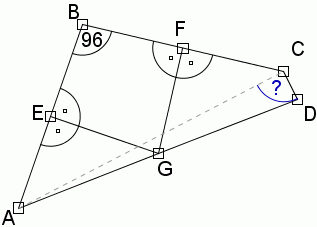
3.Zobaczmy, czy na czworokącie ABCD można opisać okrąg:

a)Punkt G dzieli odcinek AD na dwie równe części, więc AG=GD. Oznaczamy te odcinki przez x.

b)Łączymy ze sobą punkty B i G oraz oznaczamy ten odcinek przez y:

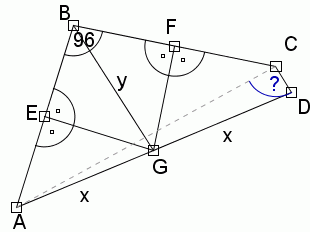
Teraz możemy zauważyć, że trójkąty AGE i GEB są przystające, co wynika z cechy bkb, gdyż punkt E jest środkiem odcinka AB, więc odcinki AE i AB są tej samej długości, odcinek GE jest prostopadły do AB, czyli te trójkąty mają ten sam kąt 90°oraz wspólny odcinek GE.

Stąd wynika, że x=y

c)Łączymy punkt G z C i oznaczamy ten odcinek przez z:

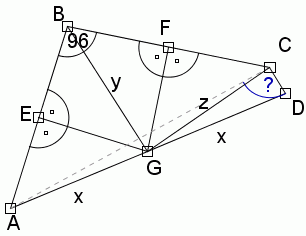
Z cechy bkb wynika, że trójkąty BGF i GFC są przystające, ponieważ F jest środkiem odcinka BC, więc te odcinki są równej długości, GF jest prostopadłe do BC, więc te trójkąty maję kąt prosty oraz wspólny bok, którym jest odcinek GF.

Stąd wynika, że x=y=z.

Zatem na czworokącie ABCD można opisać okrąg o środku G i promieniu równym x, który wynosi tyle samo co y oraz z; x=y=z, więc punkty ABCD będą leżały na okręgu.

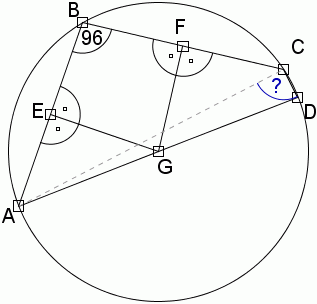
Możemy zauważyć, że kąt ACD jest kątem wpisanym opartym na średnicy okręgu, więc na podstawie twierdzenia o kącie wpisanym opartym na średnicy, wiemy że miara tego kąta wynosi 90°

Odpowiedź:

Miara kąta ACD wynosi 90°.

Ewelina Rudnicka