LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA NIESPODZIANKI NA ETAP IV
DLA KLAS I GIMNAZJUM

Zadanie 5

Wyznaczyć wszystkie liczby pierwsze p tak, aby liczba p² + 11 miała dokładnie 6 dzielników.

Rozwiązanie

Liczba p² + 11 - musi mieć 6 dzielników.
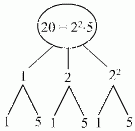
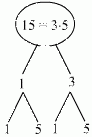Jednak aby tak mogło być musimy w rozkładzie na czynniki pierwsze otrzymać jeden kwadrat i jedną liczbę w pierwszej potędze:

p² + 11 = a² × b

gdzie a, b są liczbami pierwszymi.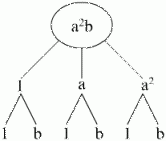

Mnożąc dzielniki wzdłuż gałęzi otrzymujemy wszystkie dzielniki liczby a² × b:
1, b, a, a× b, a², a² × b.

Jeśli p = 2, to p² + 11 = 2² + 11 = 15 = 3 × 5
Liczba 15 ma tylko 4 dzielniki:
1 × 1 =1,
1 × 3 = 3,
1 × 5 = 5,
3 × 5 = 15
więc nie spełnia warunku zadania.

Jeśli p = 3, to p² + 11 = 3² + 11 = 20 = 2² × 5
Liczba 20 ma tylko 6 dzielników:
1 × 1 =1,
1 × 5 = 5,
2 × 1 = 2,
2 × 5 = 10
2² × 1 = 4
2² × 5 = 20
więc spełnia warunek zadania.

Jeśli p ą 2 i p ą 3, to
(a) p² + 11 dzieli się przez 4, tzn. przez 2² (patrz: dowód)

(b) p² + 11 dzieli się przez 3 (patrz: dowód)
więc biorąc pod uwagę, że
p² + 11 = a² × b,
gdzie a, b są liczbami pierwszymi,

musiałaby zachodzić równość:
p² + 11 = 2² × 3
a to jest niemożliwe bo wtedy p = 1 nie jest liczba pierwszą.

Odpowiedź

Liczba p² + 11 ma 6 dzielników tylko dla liczby pierwszej p = 3.